[암호학](-)[RSA 구현 2]

이전 글: https://verybigsilver.tistory.com/106

[암호학](-)[RSA 구현 1]

 

GMP 라이브러리를 이용한 RSA 구현

예전에 짰던 RSA 프로그램은 파이썬이나 C로 짰었는데,
파이썬은 시간이 너무 오래 걸리고
C는 visual studio 기준으로 long long 64비트밖에 지원을 하지 않아서 오버플로우가 났었다.

따라서 C에서 큰 수의 연산을 가능하게 하는 GMP 라는 라이브러리로 다시 구현해 보겠다.

 

GMP 라이브러리는 mpz_t라는 엄청 큰 자료형을 지원하고 그걸 위한 연산도
단순히 +, * 이런게 아니라
mpz_mul 처럼 전용 함수로 계산해야 한다.
내장으로 mpz_gcd 같은 모듈이 있긴 한데 그냥 만들어 둔 함수 안에 모듈 넣어서 처리했다.

 

또한 컴파일 시 -lgmp로 컴파일해야 한다

근데 윈도우에선 gmp를 깔고 환경 설정하기엔 복잡하므로

그냥 리눅스로 gmp 깔고 돌려봤다.

gcc RSA.c -o RSA -lgmp

 

구현

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <gmp.h>

// 최대공약수
void gcd(mpz_t result, const mpz_t a, const mpz_t b) {
    mpz_gcd(result, a, b);
}

// 소수 판별
int is_prime(const mpz_t x) {
    return mpz_probab_prime_p(x, 15); // Miller-Rabin test 반복횟수
}

// 다음 소수 찾기
void next_prime(mpz_t res, const mpz_t n) {
    mpz_nextprime(res, n);
}

// 랜덤한 서로소
void random_coprime(mpz_t result, const mpz_t phi) {
    gmp_randstate_t state;
    gmp_randinit_default(state);
    gmp_randseed_ui(state, time(NULL));

    mpz_t candidate;
    mpz_init(candidate);

    do {
        mpz_urandomm(candidate, state, phi);
        mpz_add_ui(candidate, candidate, 2);
        gcd(result, candidate, phi);
    } while (mpz_cmp_ui(result, 1) != 0);

    mpz_set(result, candidate);
    mpz_clear(candidate);
    gmp_randclear(state);
}

// 확장 유클리드 (역원 구하기)
void modinv(mpz_t result, const mpz_t a, const mpz_t m) {
    mpz_invert(result, a, m); // 존재하지 않으면 0 반환됨
}

// 지수승 모듈러
void mod_pow(mpz_t result, const mpz_t base, const mpz_t exp, const mpz_t mod) {
    mpz_powm(result, base, exp, mod);
}

// 두 개의 소인수 찾기
int prime_factor(const mpz_t n, mpz_t p, mpz_t q) {
    mpz_t i, sqrt_n, rem;
    mpz_inits(i, sqrt_n, rem, NULL);

    mpz_sqrt(sqrt_n, n);
    mpz_set_ui(i, 2);

    while (mpz_cmp(i, sqrt_n) <= 0) {
        mpz_mod(rem, n, i);
        if (mpz_cmp_ui(rem, 0) == 0) {
            mpz_set(p, i);
            mpz_div(q, n, i);
            mpz_clears(i, sqrt_n, rem, NULL);
            return 1;
        }
        mpz_add_ui(i, i, 1);
    }

    mpz_clears(i, sqrt_n, rem, NULL);
    return 0;
}

int main() {
    mpz_t p, q, m, phi, k, msg, cipher, decrypted, u;
    mpz_inits(p, q, m, phi, k, msg, cipher, decrypted, u, NULL);

    unsigned int hardness;
    printf("hardness (bit): ");
    scanf("%u", &hardness);

    char msg_str[1024];
    printf("보낼 메시지(정수): ");
    scanf("%s", msg_str);
    mpz_set_str(msg, msg_str, 10);

    gmp_randstate_t rstate;
    gmp_randinit_default(rstate);
    gmp_randseed_ui(rstate, time(NULL));

    // 소수 생성
    do {
        mpz_urandomb(p, rstate, hardness);
        next_prime(p, p);

        mpz_urandomb(q, rstate, hardness);
        next_prime(q, q);
    } while (mpz_cmp(p, q) == 0);

    // 공개 파라미터
    mpz_mul(m, p, q);
    mpz_sub_ui(p, p, 1);
    mpz_sub_ui(q, q, 1);
    mpz_mul(phi, p, q);
    mpz_add_ui(p, p, 1); // p, q 복원
    mpz_add_ui(q, q, 1);

    random_coprime(k, phi);

    gmp_printf("공개 파라미터:\nm = %Zd\nk = %Zd\n", m, k);

    // 암호화
    mod_pow(cipher, msg, k, m);
    gmp_printf("암호문 = %Zd\n", cipher);

    // 복호화 시작
    clock_t start = clock();

    if (!prime_factor(m, p, q)) {
        printf("소인수분해 실패\n");
        return 1;
    }

    mpz_sub_ui(p, p, 1);
    mpz_sub_ui(q, q, 1);
    mpz_mul(phi, p, q);

    modinv(u, k, phi); // 역원 구하기

    // 복호화
    mod_pow(decrypted, cipher, u, m);
    gmp_printf("복호문 = %Zd\n", decrypted);

    clock_t end = clock();
    double elapsed_time = (double)(end - start) / CLOCKS_PER_SEC;
    printf("실행 시간 = %f 초\n", elapsed_time);

    mpz_clears(p, q, m, phi, k, msg, cipher, decrypted, u, NULL);
    gmp_randclear(rstate);

    return 0;
}

 

또한 hardness를 더 골치아프게 변경했다

 do {
        mpz_urandomb(p, rstate, hardness);
        next_prime(p, p);

        mpz_urandomb(q, rstate, hardness);
        next_prime(q, q);
    } while (mpz_cmp(p, q) == 0);

단순히 자릿수 연산인 hardness에서
mpz_urandomb로 소수를 생성하게 했다.

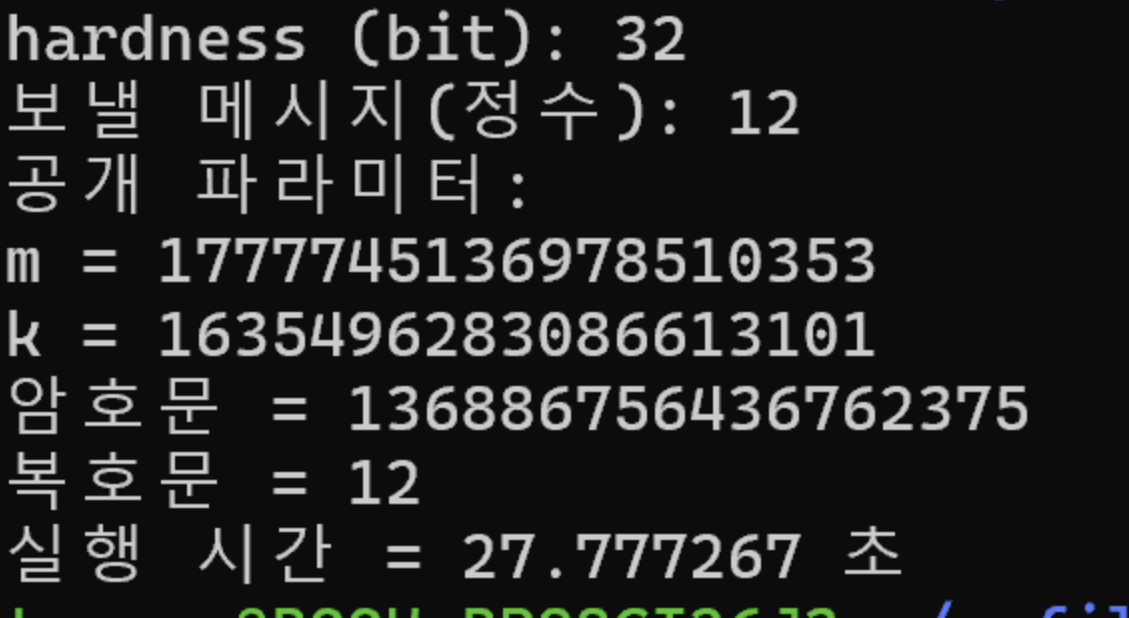
확실히 자릿수가 뻥튀기 된다.

hardness	시간
4 bit	0.000013 초
8 bit	0.000018 초
16 bit	0.000498 초
32 bit	27.777267 초
35 bit	936.152368 초 = 약 15~16분
64 bit	인내심의 한계

아래는 몇가지 예시를 첨부한다.

hardness (bit): 4
보낼 메시지(정수): 12
공개 파라미터:
m = 187
k = 59
암호문 = 23
복호문 = 12
실행 시간 = 0.000013 초

===========================

hardness (bit): 8
보낼 메시지(정수): 12
공개 파라미터:
m = 40349
k = 31675
암호문 = 10060
복호문 = 12
실행 시간 = 0.000018 초

============================

hardness (bit): 16
보낼 메시지(정수): 12
공개 파라미터:
m = 188637233
k = 173808937
암호문 = 39087002
복호문 = 12
실행 시간 = 0.000498 초

============================

hardness (bit): 32
보낼 메시지(정수): 12
공개 파라미터:
m = 1777745136978510353
k = 1635496283086613101
암호문 = 136886756436762375
복호문 = 12
실행 시간 = 27.777267 초

============================

hardness (bit): 35
보낼 메시지(정수): 12
공개 파라미터:
m = 202589604157568020703
k = 2550875862200761349
암호문 = 34722827211541514032
복호문 = 12
실행 시간 = 936.152368 초