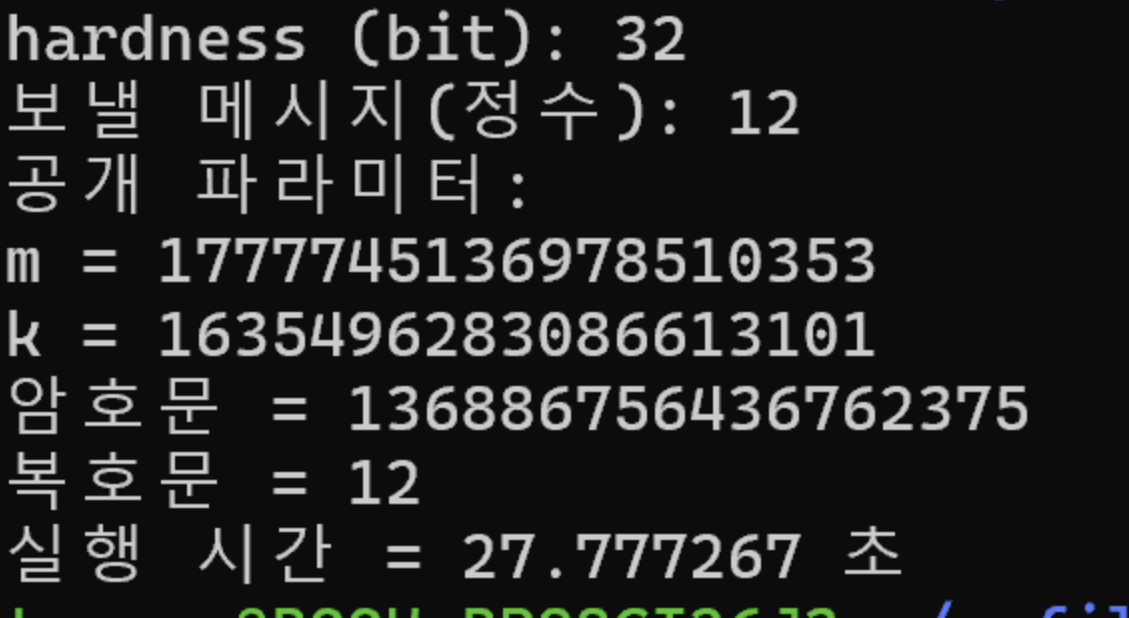
정수론 수업을 듣고 흥미로운 문제를 들었다.n차 합동방정식은 n개의 서로 다른 해를 가지는데 왜 RSA는 복호화가 잘 되는가?이거에 대해 알아본 결과.A를 특정 값으로 제한해서 복호화가 망가지는 걸 억제하는 것이였다. A값의 제한으로 여러 해 나오지 않게 하기m = pq (p, q는 소수)gcd(ϕ(m), k) = 1 에서 암호화는 c ≡ a^k (mod m) 이다.당연히 c는 양수(암호문은 항상 양수만 생각)이고 m에 대해 유일하다. 그럼 문제의 복호화는?x ≡ c^u ≡ a (mod m) 이다.이때 gcd(ϕ(m), k) = 1 이므로 선형방정식의 정리에 의해ku-ϕ(m)v = 1에서 해 ui, vi를 구할 수 있고 식을 변형하면 ku ≡ 1 mod(ϕ(m))이다.gcd(ϕ(m), k) = 1이므로 ..

이전 글: https://verybigsilver.tistory.com/106 [암호학](-)[RSA 구현 1]이론 암호학 중심 이론 정리https://verybigsilver.tistory.com/55 [암호학 둘러보기](8)[RSA]RSA: 비대칭키 암호화 방식디피-헬만과는 다르게 서명까지 지원해 안전함. (상대방의 공개키를 이용해 암호화하기verybigsilver.tistory.com GMP 라이브러리를 이용한 RSA 구현예전에 짰던 RSA 프로그램은 파이썬이나 C로 짰었는데,파이썬은 시간이 너무 오래 걸리고C는 visual studio 기준으로 long long 64비트밖에 지원을 하지 않아서 오버플로우가 났었다.따라서 C에서 큰 수의 연산을 가능하게 하는 GMP 라는 라이브러리로 다시 구현해 보..

이론 암호학 중심 이론 정리https://verybigsilver.tistory.com/55 [암호학 둘러보기](8)[RSA]RSA: 비대칭키 암호화 방식디피-헬만과는 다르게 서명까지 지원해 안전함. (상대방의 공개키를 이용해 암호화하기 때문)과정메세지 보내는 A, 메세지 받는 B이고 공개된 파라미터 e가 있다.B의 공verybigsilver.tistory.com 수론 중심 이론 정리https://verybigsilver.tistory.com/100 참고 구현 일단 코드를 대충 짜면 이렇게 된다.def extended_gcd(a, b): if b == 0: return 1, 0 # 해는 (1, 0) x1, y1 = extended_gcd(b, a % b) # 재귀 호출 ..

비대화형 ZKP: 지식 증명할 때 상호작용 없음 (증거(x1, x2)를 딱 한번만 전송)과정메세지가 m^e = c (mod N)로 암호화 됨. (e, c, N은 공개됨) 이때 m을 공개하지 않고 m을 알고 있다는 걸 증명이후 검증자가 계산할 때 x1*x2 = c (mod N) 라면 검증 성공(공개/전송된 파라미터에서 에서 m을 알아내긴 어려워 증명자는 m을 밝히지 않고 m을 알고있다 증명 가능!)임의의 정수 r1을 선택(공개x), 이후r2 = m * r1^(-1) (mod N)x1 = r1^e (mod N)x2 = r2^e (mod N)에서 계산된 (x1, x2)를 전송이후 검증자가 계산할 때 x1\*x2 = c (mod N) 라면 검증 성공(공개/전송된 파라미터에서 에서 m을 알아내긴 어려워 증명자는 ..

영지식 증명: 상대에게 구체적인 내용은 알리지 않은 채 어떤 주장을 참이라는 걸 증명하는 방법완전성: 주장이 참이라면 항상 증명을 받아들일 수 있다건실성: 주장이 거짓이라면 증명자가 검증자를 속일 확률이 매우 낮다영지식성: 검증자는 주장이 참이라는 사실만 알 수 있지 그 외의 정보는 모른다대화형 ZKP: 지식을 증명할 때 상호작용 있음 (증거를 여러번 전송)과정p는 매우 큰 소수, g는 Zp의 생성자B = g^a (mod p)로공개 피라미터 (p, g, B)를 합의한다증명자는 w = (k - a*r) (mod p-1)을 통해 w를 계산하고 전달한다.만약 V = g^w * B^r (mod p)가 만족한다면 검증 성공이 과정을 여러번 반복해 증명자가 a를 알고 있을 확률을 높인다.증명자는 임의의 정수 k (..

ElGamal 서명: D-H 알고리즘의 발전형디피-헬만 알고리즘에서 사용했던 (g, p, y)를 사용하면서 서명기능까지 있다!과정큰 소수 p와, g, 비밀키 x선택 (단, 1y = g^x (mod p) 계산공개키: (p, g, y), 개인키: x이후 서명 검증y^r*r^s (mod p)= g^M' (mod p)라면 유효함서명(r, s)해싱: M -> M'랜덤값 k를 선택 (단 1 r = g^k (mod p)s = k^(-1)(M' - xr) (mod p-1) (단, k^(-1)은 mod p-1에서 곱셈 역원)예앨리스가 밥에게 서명과 메세지를 보낸다고 한다. 파라미터는 g = 7, p = 11을 합의해놨다. (편의를 위해 작은 소수로 정함.)앨리스의 개인키 = 3, 밥의 개인키 = 4앨리스의 공개키 = 7..

디지털 서명: 메세지는 서로만, 그러나 증명은 아무나 할 수 있게역할송신자의 신원 증명메세지가 중간에 조작되지 않았단 증명메세지를 자신이 보냈다는 걸 부인하지 않게 하는 증명RSA 서명이전에 RSA를 사용할 땐 앨리스만 개인키를 정했으나, 디지털 서명에서는 송신자인 밥도 소수 2개를 고르고 공개키, 개인키를 생성한다.이후 밥은 보낼 메세지를 해시로 바꾸고 공개한다.공개된 메세지 해시에 개인키로 서명을 한다.밥의 공개키로 서명을 복호화하고, 만약 이것이 메세지 해시와 같다면 이 메세지는 밥이 보낸거라 할 수 있다.예)암호학 둘러보기 9 참고공개 파라미터(7), 보내는 메세지(8) 등 이전 RSA와 동등한 조건이라 가정할 떄,이전과 같이 밥은 앨리스의 공개키(N)으로 암호화: C = 8^7 (mod 15) ..

해시 함수: 임의의 입력을 고정된 길이로 출력하는 함수h(M) = M'(해시 출력값)특징해시 함수로 나온 출력으로 입력을 예측하기 어렵다.같은 해시값을 갖는 서로 다른 입력값을 찾기 힘들다. (충돌 x)같은 입력을 넣는다면 출력도 당연히 같다.이산로그에 비해 해시는 매우 빠르다.쓰임디지털 서명: 원본 메세지 노출 없이 서명을 받을 수 있음메세지 무결성 검정: 메세지의 일부만 변경해도 해시값은 천차만별로 달라져 메세지가 수정되었는지 검증 가능데이터베이스 인덱싱종류: MD5, SHA, CRC 등...SHA-1: 가장 간단한 SHA 알고리즘반복적 연산으로 160비트의 해시를 출력한다.과정데이터 처리: 입력 데이터를 512의 배수로 만들기 (모자르면 패딩)초기 해시값: 가장 처음엔 이 값이 저장되어있음    레..

RSA: 비대칭키 암호화 방식디피-헬만과는 다르게 서명까지 지원해 안전함. (상대방의 공개키를 이용해 암호화하기 때문)과정메세지 보내는 A, 메세지 받는 B이고 공개된 파라미터 e가 있다.B의 공개키(N): N = p*q (p, q는 매우 큰 소수)B의 개인키([d]): [d]*e = 1 (mod[p-1]*[q-1]) (모듈러 역원 구하기. 만족하는 정수 d는 1개밖에 없으니 안심)A가 보낼 메세지 암호화(C): C = M^e (mod N)B는 자신의 개인키로 복호화(M): M = C^[d] (mod N)예)밥이 앨리스에게 8이란 메세지를 보낼 때, e = 7이라는 파라미터로 합의했다.앨리스는 비밀스럽게 p = 3, q = 5라 정했다. (원래 p, q는 큰 소수이지만 예시라 간단한 수 사용함.)공개키:..

비대칭키 암호: 서로 다른 키를 이용해 메세지를 암호화, 복호화하는 암호    서로 같은 키를 사용해 암호화하는 대칭키 암호에서 키가 중간에 탈취되어 암호가 뚫리는 문제를 해결함. (직접 키 교환이 아니라 각자 가지고 있는 키로 암호/복호화) 모듈러 연산: 나머지 연산 %    예) 4 (mod 3) = 1이산 로그: 이산 거듭제곱 계산은 쉽지만 역방향인 이산 로그는 어렵다는 것을 이용    모듈러 연산에 닫혀있는 Zp에 대해 g^x (mod p) = y 는 쉽지만 g, p, y를 가지고 x를 계산하긴 어렵다.    특히 p가 커질수록 순환군의 크기도 커지므로 계산이 더 어려워진다.    예) g = 2, x = 3, p = 7        y = 2^3 (mod 7) = 8 (mod 7) = 1    ..